Posts from — November 2008

To me, an intermediate and somewhat casual Mathematica user, the news that Mathematica 7 had been released was a surprise. Surprising to me because Mathematica usually goes much longer between major-digit releases; I would have anticipated this to be Version 6.1. For fun, I’ve plotted the history of Mathematica versions¹ :

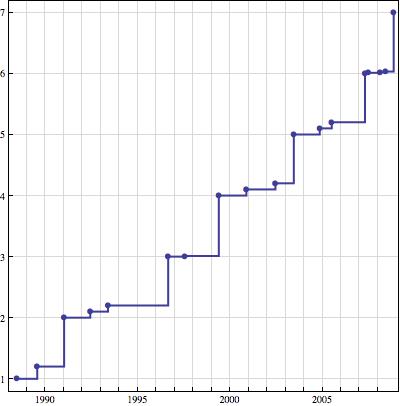
Release dates of versions of Mathematica

Mathematica 6 was a substantial upgrade: the graphics system was completely overhauled, the curated data, that I’ve used as the basis for some posts here, was added, and the ability for dynamic interactivity was added with Manipulate and Dynamic. 

I am not, of course, a major Mathematica user. In fact, although I’m a physicist, I haven’t made tremendously much use of Mathematica for my professional work. This is partly because I tend to deal with relatively small data sets, for which a GUI-based data analysis tool is usually easier to work with than the command-line Mathematica. And I’d consider myself an advanced user of Pro Fit, the data analysis tool that’s made all the graphs for all the work I’ve done since about 1998.

In fact, my Mathematica license is my own personal one. As a graduate student, I bought the Student version of Mathematica, which they allow you to upgrade to a full professional license for only a few hundred dollars, compared to the $2500 list price of a new professional license.

Wolfram really wants its users to buy Premier Service, a several hundred dollars per year service which entitles you to all upgrades, major and minor. If you don’t buy premier service, then you need to pay for all upgrades, even the N.M.X to N.M.X+1 minor bug-fixing upgrades. And without premier service, you’re not even supposed to install Mathematica on more than one computer. Draconian and greedy, if you ask me, but they can do that, because they’re Wolfram. And for tech-heavy firms that make heavy use of Mathematica and get millions of dollars worth of value from whatever they compute in Mathematica, it makes sense. But it makes it very difficult to be a casual user.

And even though your existing copy can do everything it could the day you bought it, once the difference between your copy and the current release gets large enough, there is no longer an upgrade path. I think this is one of the motivations to release this as version 7 and not 6.1: I don’t recall the precise figure, but Wolfram generally offers an upgrade path only for jumps smaller than 1.5. If this is still the case,² what this does is cut off anyone who hadn’t upgraded to version 6. Update: enough with the conspiracy theories! Wolfram clears up the upgrade policy in the comments.

In my case, with Version 6.0.1, I have a choice of paying $750, and getting a year of Premier Service, or paying $500 for just version 7.0.0 with no service. Out of my own pocket, ouch! But what makes it really enticing, for me, is that Mathematica now reads SHP files. These are the Geographic Information System data files, promulgated by ESRI, in which vector-valued geographic data is commonly exchanged. In particular, the DC Office of Planning makes an amazingly large collection of DC GIS data available in SHP format. The possibility for quantitative analysis of DC mapping data is very tantalizing.

Of course, Wolfram wouldn’t release a major number upgrade without hundreds of other new features. As of yet, there isn’t much substantial written about version 7. I did find some notes from a beta-tester and from a college math teacher. I’ll probably buy it, even though it would mean delaying other expensive toys that I want.

1. most of the dates come from the Wolfram News Archive, some from the Mathematica scrapbook pages [↩]
2. I’ve asked Wolfram, but haven’t received a reply. [↩]

I needed to buy more gasoline for the car today, and I decided to see how long it took to fill the tank. I bought ten and a half gallons of gas, and it took 70 seconds to fill it up. Although filling up a gas tank is something that millions of Americans do every day, it’s really remarkable when you stop and think about the energy transfer going on.

Gasoline has, approximately, 113,000 BTUs per gallon.¹ One BTU is 1055 Joules. So I transferred 1.25 Billion Joules in those 70 seconds, which is a rate of 17.9 megawatts. When you consider that you spend less than two minutes pumping the same amount of energy you burn in four hours of driving, it’s not surprising that you end up with such a high power. What’s more interesting, I think, is to contemplate the rather fundamental limits this puts on plug-in electric cars.

Internal combustion engines, according to Wikipedia, are only about 20% efficient, which is to say, for every 100 BTUs of thermal energy consumed by the engine, you get 20 BTUs of mechanical energy out. This is, in large part, a consequence of fundamental thermodynamics. Although electric motors can be pretty close to perfectly efficient, a similar thermal-to-electric efficiency hit would be taken at the power plant.

Let’s consider, then, that we want a similar car to mine, but electric. Instead of 1.25 gigajoules, we need to have 250 megajoules. Battery charging can be pretty efficient, at 90% or so, which means we’d supply 280 megajoules. If we expect the filling-up time to be comparable to that of gasoline cars–call it 100 seconds for simplicity–then we’d need to supply 2.8 megawatts of power. At 240 Volts, which is the voltage we get in our homes, this would require 11700 amps; if you used 1000 Volts, it would take 2800 amps. Although equipment exists² to handle these voltage and current levels, it is an understatement to say that it cannot be handled as casually as gasoline pumps are handled. Nor is it clear that any battery system would actually be able to accept this much power.

A linear relationship exists between the power requirement for filling, and the vehicle range, the vehicle power, and the time for a filling. If you’re satisfied with half the range of a regular vehicle, for example, you could use half the filling power. Let’s imagine that you’d be happy for the filling to take ten times as long as with gasoline, or 1000 seconds, just under 17 minutes. At this level, you’d need 280 kilowatts of power. If battery charging is 90% efficient, that means 10% of the power is going to be dissipated as heat, which in this case would be 28 kilowatts.

For comparison, a typical energy consumption rate for a home furnace is 100,000 BTU per hour, about 28 BTU per second, or 29.3 kilowatts. Which means that the waste heat dissipated during charging for the example–of a 1000 second fill for a vehicle with similar range and power as a modest gasoline powered sedan, at 90% charging efficiency–is as much as the entire output of a home furnace.

No wonder overnight charges are the standard.

1. Summer and winter blends have slightly more and less, respectively. [↩]
2. think about how large the wires would need to be [↩]

Part 1 of this series looked at the beginnings of the DC government’s effort to expand the transit network. We left off in the Spring of 2005, having been to several meetings and having received several newsletters.

The study finishes

The final project newsletter, Fall 2005, and an “Executive Summary” of the whole project were presented to the public at a final meeting, held September 29, 2005. For transit enthusiasts following the project, the end results were disappointing and frustrating. Instead of a visionary transformation of mobility in the District, the final recommendations proposed a meager streetcar buildout that, despite its modest size, would take 25 years to build. The report was frustrating because it relied on tortured reasoning that bordered on downright dishonesty, it used self-contradictory and mutually inconsistent reasoning, and offered little more than poorly-defined chimeras wrapped up in wishful thinking.

Added to the project was “Rapid Bus,” as a lower-class technology mode, joining streetcars and “bus rapid transit.” Modes were assigned to routes. The newsletter used separate streetcar and “bus rapid transit” assignments, while the executive summary lumped these together as “premium transit.” In the newsletter, streetcars got a handful of routes: the crosstown Georgtown to Minnesota Avenue route; the north-south Georgia Avenue route, which would end at K street; a Union Station to Anacostia via Eastern Market route; an M Street SE/SW route, and a short Bolling AFB–Pennsylvania Ave route. A bit of “bus rapid transit” was added: mainly Woodley Park to Eastern Market via Florida Avenue, while the rest of the 50-mile route structure developed over the course of the study was designated “rapid bus.”

[Read more →]

A recent post by economist-blogger Brad DeLong, which was also picked up Matthew Yglesias, mused upon the clustering of the Dow Jones Industrial Average clustered near values starting with 1. He showed a chart with the years 1971–1984, and 1996–2008 circled, when the Dow appeared to fluctuate near 1000 and 10000, respectively. Many commenters quickly jumped to point out that this was an example of Benford’s Law, which says, essentially, that if you’re throwing darts at a logarithmically shaped dartboard, you’re going to hit “1” more often than any other digit. If you pick random values of some phenomenon that is logarithmically distributed, you should get values beginning with “1” about 30% of the time, which makes sense if you’ve ever looked at log scale graph paper.

It occurred to me that this is an easy thing to investigate with Mathematica, much like my earlier post on the Bailout. Mathematica 6 includes access to a huge library of curated data, including historical values of the Dow Jones Industrial average and other indices (and individual stocks, and so forth). The function here is FinancialData, which Wolfram cautions is experimental: I believe they get the data from the same source as, say, Yahoo! Finance, and just do the conversions to make it automatically importable into Mathematica. That is, it is no more reliable than other web-based archives. The computations are absurdly easy, taking only a few lines of Mathematica code. 

The graph I (eventually) produced shows the relative frequencies of first digits that are calculated by Benford’s Law, together with the relative frequencies of the leading digits from the Dow Jones Industrial Average, the S&P 500, the NASDAQ Composite index, the DAX 30, and the Nikkei 225:

[Read more →]