DC intersections with Mathematica

Without the quadrant designation, several intersections in Washington–“6th and C,” for example–are ambiguous. “6th and C” can refer to a place in NW, NE, SW, or SE DC. Because of this duplication of streets and intersections, the quadrant is usually–but not always–specified. I’ve been curious  for some time to know exactly how many doubly-, triply-, and quadruply-redundant intersections there are in DC, and it’s another fun example combining Mathematica 7‘s .shp file import with the GIS data that the DC government makes available.

How many are there? I calculate:

The 28 intersections that appear in all 4 quadrants are:

14th & D, 9th & G, 7th & I, 7th & E, 7th & G, 7th & D, 6th & C, 6th & G, 6th & D, 6th & I, 6th & E, 4th & M, 4th & G, 4th & E, 4th & D, 4th & I, 3rd & M, 3rd & C, 3rd & K, 3rd & D, 3rd & G, 3rd & E, 3rd & I, 2nd & E, 2nd & C, 1st & M, 1st & C, 1st & N

Plotted on a map:

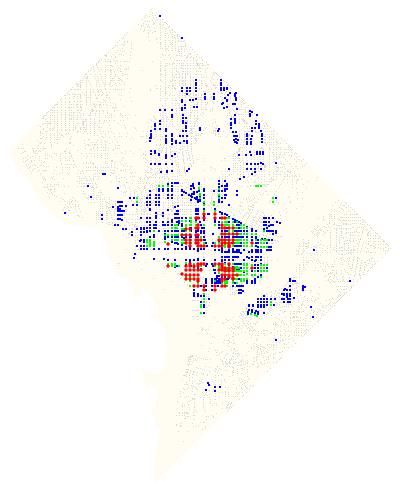
Color coded map of intersections in DC.

Update: Here’s a larger PDF version.

Here’s how I made the map and did the calculations:

I started with the same Street Centerline file that I used in my first post on GIS with Mathematica. The elements of this file are lines representing street segments between intersections, so the first and the last point defining each line lie at intersections. First, I take from the rather unwieldy raw data and make a new list where each element corresponds to one street segment, and within each of these elements, the geometry is followed by all the other data:

dcstreets=Import["StreetSegmentsLn.shp","Data"][[1]];
dcstreetdata =
Transpose[Join[{dcstreets[[2, 2]]}, dcstreets[[4, 2, All, 2]]]];

Then I wrote two functions to pick off the data I need: for each of the first and last points, representing the locations of the intersections, I need the street name, type (e.g. Street or Avenue), and quadrant:

nodeFunction = Join[{#[[1, 1, 1]]}, #[[6 ;; 8]]] &
tailFunction = Join[{#[[1, 1, -1]]}, #[[6 ;; 8]]] &
nodelist =
Union[Join[Map[nodeFunction, dcstreetdata],
Map[tailFunction, dcstreetdata]]];

Map applies the specified function to each item in the list of street segments, and the resulting lists of beginning and ending intersections from all the segments are put together with Join. Of course, most streets run through numerous intersections, and the second intersection of one segment will be the first intersection of the next segment. To make sure we get the beginning and ending of each street, we do need both the first and second intersection from each, and we use Union to remove all the duplicates from the middle.

We now have a list in which each element contains a location and street name. We now need a list of all the intersections–when two streets share the same point. Fortunately, Mathematica 7 introduced the GatherBy function, which groups a list depending on the value each element returns from the specified function. In this case, the specified function is just the first element, that is, the location:

intersections = GatherBy[nodelist, #[[1]] &];
In[]:= BinCounts[Length /@ intersections, {1, 6, 1}]
Out[]:= {901, 7015, 491, 20, 2}

The second line tells us that there are 901 end-points with only one street (the majority, I believe, are where the streets lead outside the District boundary), 7015 points where two streets come together; 491 points where three, 20 points where four, and 2 points where 5 streets come together. Which are these? With

Select[intersections, Length[#] == 5 &]

We find that the first is the intersection of 15th Street, Benning Road, Bladensburg Road, H Street, and Maryland Avenue NE, while the second is the intersection of 51st Street, Doewood Lane, Eastern Avenue, Mann Street, and Meade Street NE.¹ For our purposes, we want to consider all these as pairs, so we break all intersections with three or more streets into their respective pairs:

intersectionPairs =
Flatten[Join[Subsets[#, {2}] & /@ intersections], 1];

Since I’m using the Street Centerline File, the streets that serve as quadrant boundaries–North Capitol, East Capitol, and South Capitol streets–are not given a quadrant but given the designation “BN” for boundary. Actual addresses on these streets are given a quadrant depending on which side of the street they’re on. In this scheme, you’ll get intersections such as 17th Street NE and 17th Street SE, where they intersect East Capitol Street. I’m ignoring those for this exercise, and then using GatherBy again to find all the points where the intersection street names are the same:

quadrantPairs = Select[intersectionPairs, #[[1, 4]] == #[[2, 4]] &];
multipoint =
GatherBy[quadrantPairs, {#[[1, 2 ;; 3]], #[[2, 2 ;; 3]]} &];

Looking at the structure of this we see a little more work to be done:

In[]:= BinCounts[Length /@ multipoint, {1, 7, 1}]
Out[]:= {6287, 741, 101, 36, 7, 1}

Which tells us that there are 6287 unique intersections in DC, appearing in only one quadrant; 741 that appear in two quadrants, and 1 that appears in 6 quadrants???

This happened because Stanton Square is considered to be a giant median for C Street NE, so there are actually three distinct points that could be considered the corner of 6th and C Streets NE, all along one block. There are also intersections of 6th and C streets in NW, SE, and SW, giving a total of 6. For this, though, I want to treat all the locations in NE as the same, so I make my lists of quadruply, triply, and doubly-redundant intersections depending on how many quadrants appear, which I count with Length and Union:

quads = Select[multipoint,
Length[Union[Flatten[#[[All, All, 4]]]]] == 4 &];
triples =
Select[multipoint, Length[Union[Flatten[#[[All, All, 4]]]]] == 3 &];
doubles =
Select[multipoint, Length[Union[Flatten[#[[All, All, 4]]]]] == 2 &];

Giving lists of intersections, the lengths of which were quoted above. Relatively simple graphics commands made the figure, to which I added the DC Boundary polygon from another .shp file.

Figuring this out took far more lines of code than the modestly few lines that I can reproduce this exercise with. The keys were learning to use the new GatherBy function and getting used to the idea of Union as a list management tool, as opposed to simply part of the set theory functionality. And as usual, knowing how to use Map and pure functions are necessary for doing almost anything elegantly in Mathematica.

1. Doewood and Mann are actually the names of 51st and Meade Streets when they cross Eastern Avenue into Maryland, however I believe DC responsibility actually extends 50 feet or so beyond Eastern Avenue, hence the inclusion in the GIS data. [↩]